【基础算法】 二维前缀和——以 Leetcode 304 为例

# 题目

# 304. 二维区域和检索 - 矩阵不可变

难度：中等

给定一个二维矩阵 matrix ，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ， 右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、 右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

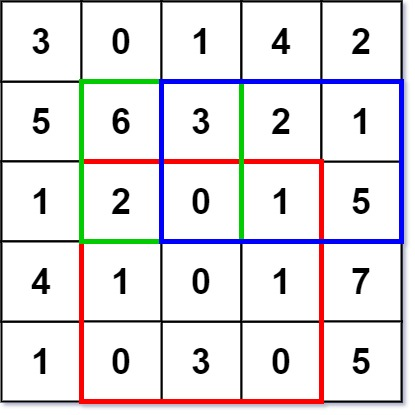
示例 1：

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -10^5 <= matrix[i][j] <= 10^5
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 10^4 次 sumRegion 方法

# 初始化各对象

给定的矩阵$matrix$ 的大小$m*n$

维护一个二维数组 sum，为了方便我们把$sum$ 的大小设置为$[m+1][n+1]$。将比$matrix$ 多出来的一行一列（$sum[0][j]和sum[i][0]$）全部初始化为 0。
存储的方法：存储矩阵$matrix$ 下标从$[0][0]$ 开始到$[i][j]$ 的子矩阵的所有元素之和到数组$sum$ 的对应位置，对应关系会在下面进行解析。

如下图：

如何实现呢？

总不能遍历 sum 直接计算对应子矩阵所有元素然后存入吧，如此麻烦，与我们追求更高效率的本心背道而驰。

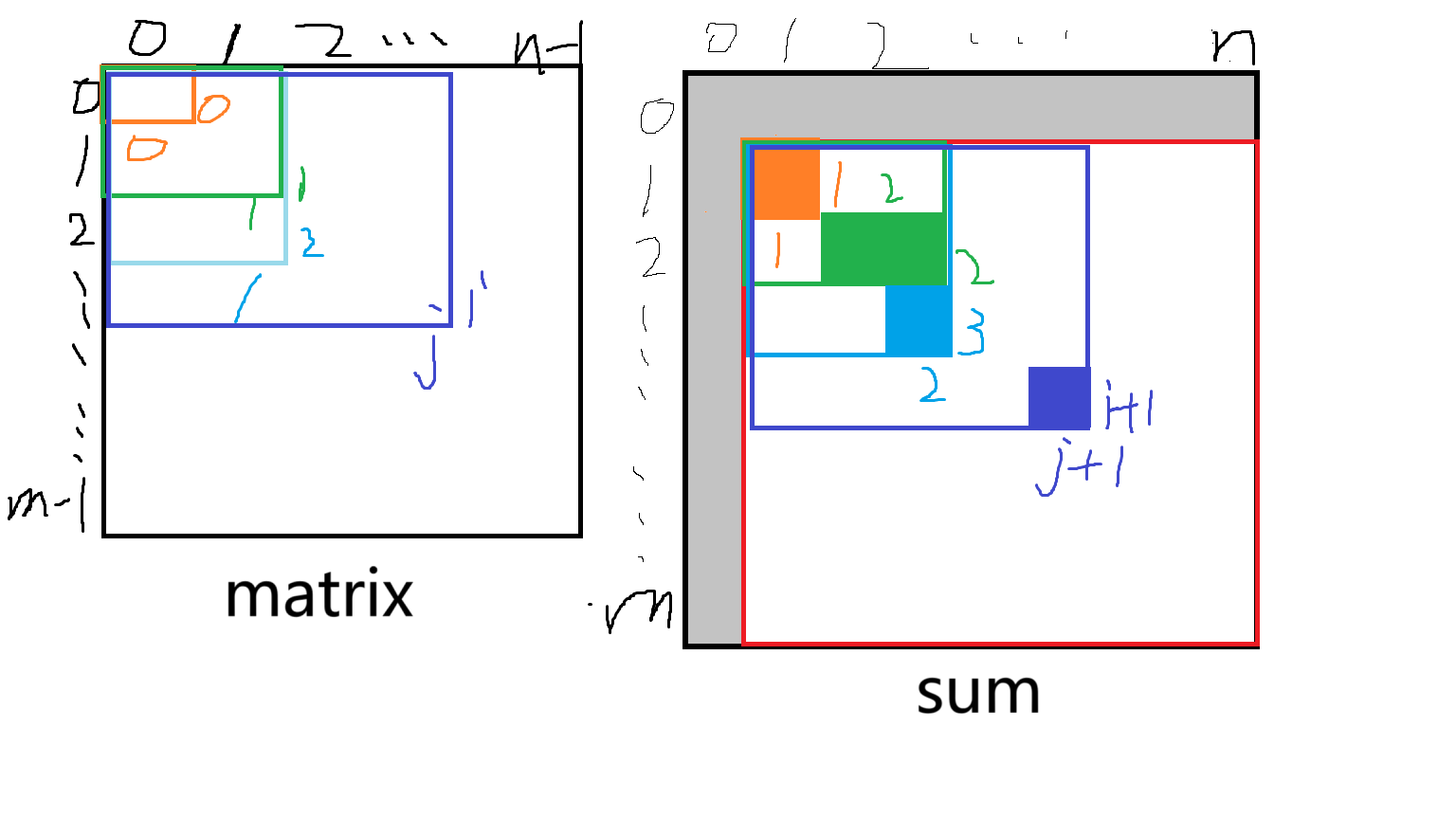
# 维护数组$sum[i][j]$

如下图，由于我们是从左到右，从上到下为$sum$ 数组赋值，所以我们可以利用已经求出来的$sum$ 的某些元素来推导出$sum[i][j]$ 的值。由原理得$sum[i][j]$ 可以看成$sum[i-1][j]$ 加上矩阵$matrix$ 的第$i$ 行计算出来的。而矩阵 matrix 的第 i 行元素之和不用遍历求出，可以使用$sum[i][j-1]-sum[i-1][j-1]$ 求出来第$i$ 行前$j$ 个元素的和，再加上$matrix[i][j]$ 即求出了该行元素和。注意这里$sum$ 的有效部分的下标从 1 开始，所以应该加上$matrix[i-1][j-1]$。

因此$sum[i][j]$ 可被赋值为

sum[i][j]=sum[i-1][j]+(sum[i][j-1]-sum[i-1][j-1])+matrix[i-1][j-1]

这个结论也解释了为什么$sum$ 的有效部分下标从 1 开始，这样相当于抽象出来了$matrix$ 的第$-1$ 行和第$-1$ 列，假若下标从$0$ 开始这个结论就不适用于$matrix$ 下标$i$ 或$j$ 为$0$ 的情况了，这时$i-1$ 或$j-1$ 是$-1$，是无效的下标，程序会报错。主要就是解决$matrix[0][0]$ 到$matrix[i][0]$ 和$matrix[0][j]$ 这若干区间元素和的计算使它也满足上面推导出的式子，而无需做特判。可以理解为为$matrix$ "添加" 了下标为$-1$ 的行和下标为$-1$ 的列，$sum[i][j]$ 计算的是从$matrix[-1][-1]$ 开始到$matrix[i][j]$ 的子矩阵的所有元素之和，由于下标为$-1$ 的行和下标为$-1$ 的列所有的元素都初始化为 0 了，因此$matrix[-1][-1]$ 开始到$matrix[i][j]$ 的子矩阵的所有元素之和就和从$matrix[0][0]$ 开始到$matrix[i][j]$ 的子矩阵所有元素之和相等了。经过这么转换之后$sum$ 的下标与$matrix$ 并不是一一对应的，$matrix$ 下标从$[0][0]$ 开始到$[i][j]$ 的子矩阵的所有元素之和对应的是$sum[i+1][j+1]$。

讲的稍微有些啰嗦，但是只要您把原理熟稔于心，实际写起来就远没有这么麻烦。

至此前缀和数组 sum 已经维护完毕，下面就是求本题的答案了

# 求出答案

题目要求的是给定两元素为主对角线的子矩阵所有元素之和。笔者仍然结合图片进行说明。笔者是画图苦手，这图画的略微抽象且一定程度上不合逻辑…… 一定要结合文字描述食用！

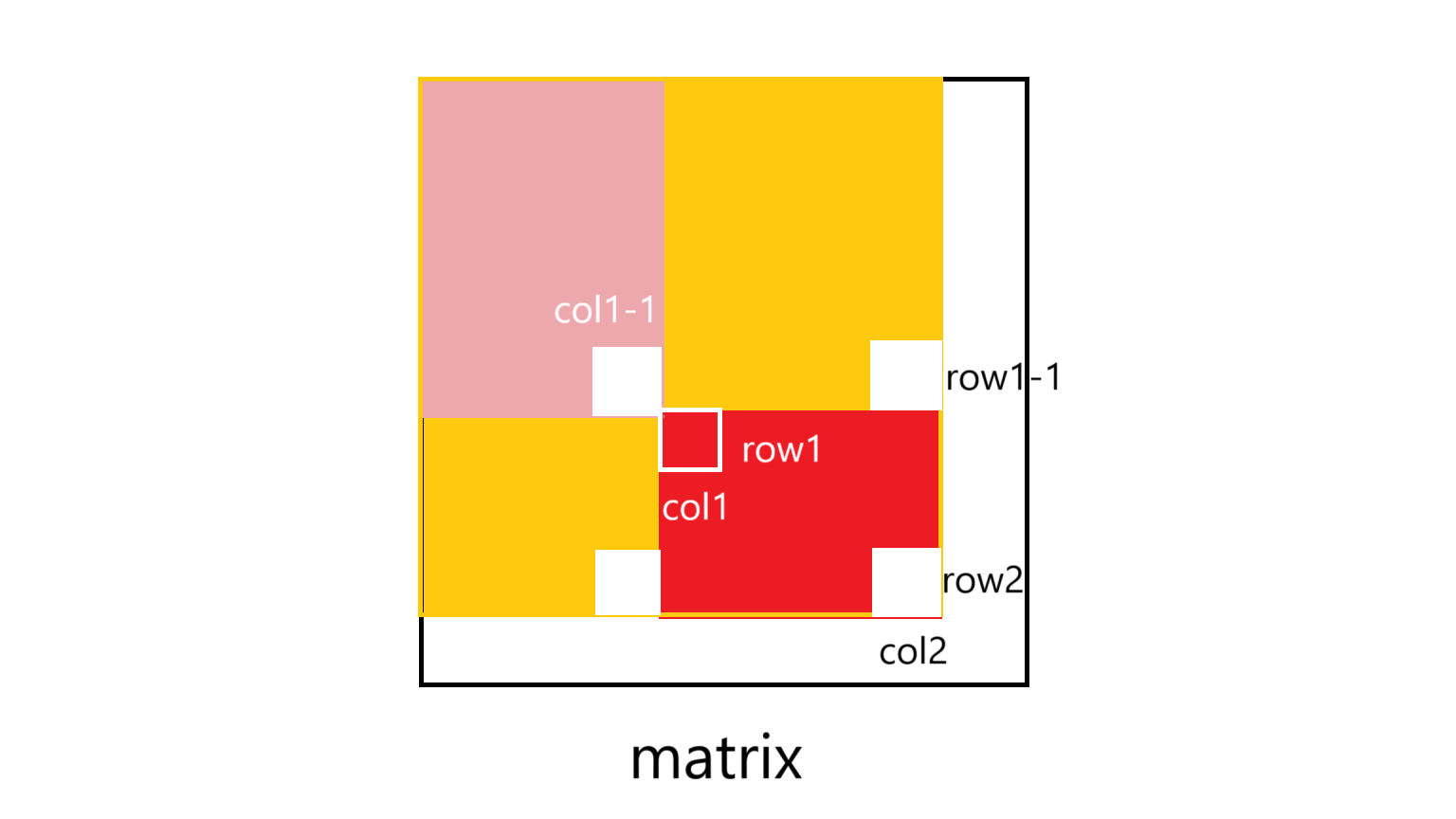
如图，将$matrix[0][0]$ 到$matrix[row2][col2]$ 这一子矩阵划为四部分。红色部分表示的为所求的子矩阵。这样就很明了了：所求子矩阵元素之和等于$matrix[0][0]$ 到$matrix[row2][col2]$ 这一子矩阵减去肉色的部分和两块黄色的部分。其中右上角黄色的部分可以表示为$sum[row1-1+1][col2+1]-sum[row1-1+1][col1-1+1]$（注意$sum$ 数组与$matrix$ 矩阵下标的转换关系，此处已做转换，下同），左下角黄色部分可以表示为$sum[row2+1][col1-1+1]-sum[row1-1+1][col1-1+1]$，诶↗，盲生你发现了华点，两个式子的减数都是 $sum [row1-1+1][col1-1+1]`，这不就是肉色的部分吗！也就是在计算两块黄色部分的时候，肉色部分已经总共被减了两次。因此表达式可写为如下形式：

res=sum[row2+1][col2+1]-sum[row1][col2+1]-sum[row2+1][col1]+sum[row1][col1];

直接把结果 return 就好了。

完整 AC 代码如下：

class NumMatrix {

public:

    vector<vector<int>> sum;

    NumMatrix(vector<vector<int>>& matrix) {

        int m=matrix.size();int n=matrix[0].size();

        sum.resize(m+1,vector<int>(n+1,0));

        for(int i=1;i<=m;i++){

            for(int j=1;j<=n;j++){

                sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+matrix[i-1][j-1];

            }

        }

    }

    int sumRegion(int row1, int col1, int row2, int col2) {

        return sum[row2+1][col2+1]-sum[row1][col2+1]-sum[row2+1][col1]+sum[row1][col1];

    }

};

时间复杂度 $ O (mn) $,为维护前缀和数组 `sum`，访问的时间为$ O (1) $

# 学以致用！

再看 2024 年 11 月 18 日 Leetcode 每日一题。我们可以用二位前缀和的方法来解这道题。

# 661. 图片平滑器

难度：简单

图像平滑器 是大小为 3 x 3 的过滤器，用于对图像的每个单元格平滑处理，平滑处理后单元格的值为该单元格的平均灰度。

每个单元格的 平均灰度 定义为：该单元格自身及其周围的 8 个单元格的平均值，结果需向下取整。（即，需要计算蓝色平滑器中 9 个单元格的平均值）。

如果一个单元格周围存在单元格缺失的情况，则计算平均灰度时不考虑缺失的单元格（即，需要计算红色平滑器中 4 个单元格的平均值）。

给你一个表示图像灰度的 m x n 整数矩阵 img ，返回对图像的每个单元格平滑处理后的图像 。

示例 1:

输入:img = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[0, 0, 0],[0, 0, 0], [0, 0, 0]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0

示例 2:

输入: img = [[100,200,100],[200,50,200],[100,200,100]]
输出: [[137,141,137],[141,138,141],[137,141,137]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
对于点 (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
对于点 (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138

提示:

• m == img.length
• n == img[i].length
• 1 <= m, n <= 200
• 0 <= img[i][j] <= 255

# 解法一：直接遍历

# 思路：

不黄但很暴力，直接遍历不多解释。问就是数据量少 [doge]。

# 完整代码：

class Solution {

public:

    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {

        int m=img.size(),n=img[0].size();

        vector<vector<int>> ans=img;

        for(int i=0;i<m;i++){

            for(int j=0;j<n;j++){

                int cnt=0,res=0;

                for(int dx=i-1;dx<=i+1;dx++){

                    if(dx<0||dx>=m)

                    continue;

                    for(int dy=j-1;dy<=j+1;dy++){

                        if(dy<0||dy>=n)

                        continue;

                        res+=img[dx][dy];cnt++;

                    }

                }

                res/=cnt;

                ans[i][j]=res;

            }

        }

        return ans;

    }

};

时间复杂度为$O(m×n×k^2)$，$k$ 为平滑器的边长，题目中规定平滑器的大小为$3×3$ 数据量不算大。但是如果题目给的边长更大，那么暴力就要 TLE 了。在这个方法中有大量元素被重复用于计算求和，效率实在不高。

# 解法二：二维前缀和

# 思路：

维护一个二维数组$sum[m+2][n+2]$ 作为前缀和数组，具体维护方式和上面的一样，$sum[i][j]$ 表示的还是以$[0][0]和[i-1][j-1]$ 为主对角线两端点的子矩阵的所有元素之和。$sum[i][j]$ 赋值的方法和板子中的结论还是相同的。

接下来先介绍对$sum$ 进行分块处理求出我们想要的平滑器中元素之和。

这里我们要求的是这个 以$img[i][j]$ 为中心 的平滑器包含的所有元素的平均值，我们表示子矩阵（平滑器）的下标和前缀和数组下标的对应关系也发生了改变，要求以$img[i][j]$ 为中心的平滑器的所有元素之和，结合下图，我们要先求出从$img[0][0]$ 到$img[i+1][j+1]$ 这个子矩阵的所有元素之和即$sum[i+2][j+2]$。然后分别减去两块黄色和一块粉色部分，与板子中的方法相同。

平滑器的和的表达式为：

int Sum=sum[i+1+1][j+1+1]-sum[i-1][j+1]-sum[i+1+1][j-1]+sum[i-1][j-1];

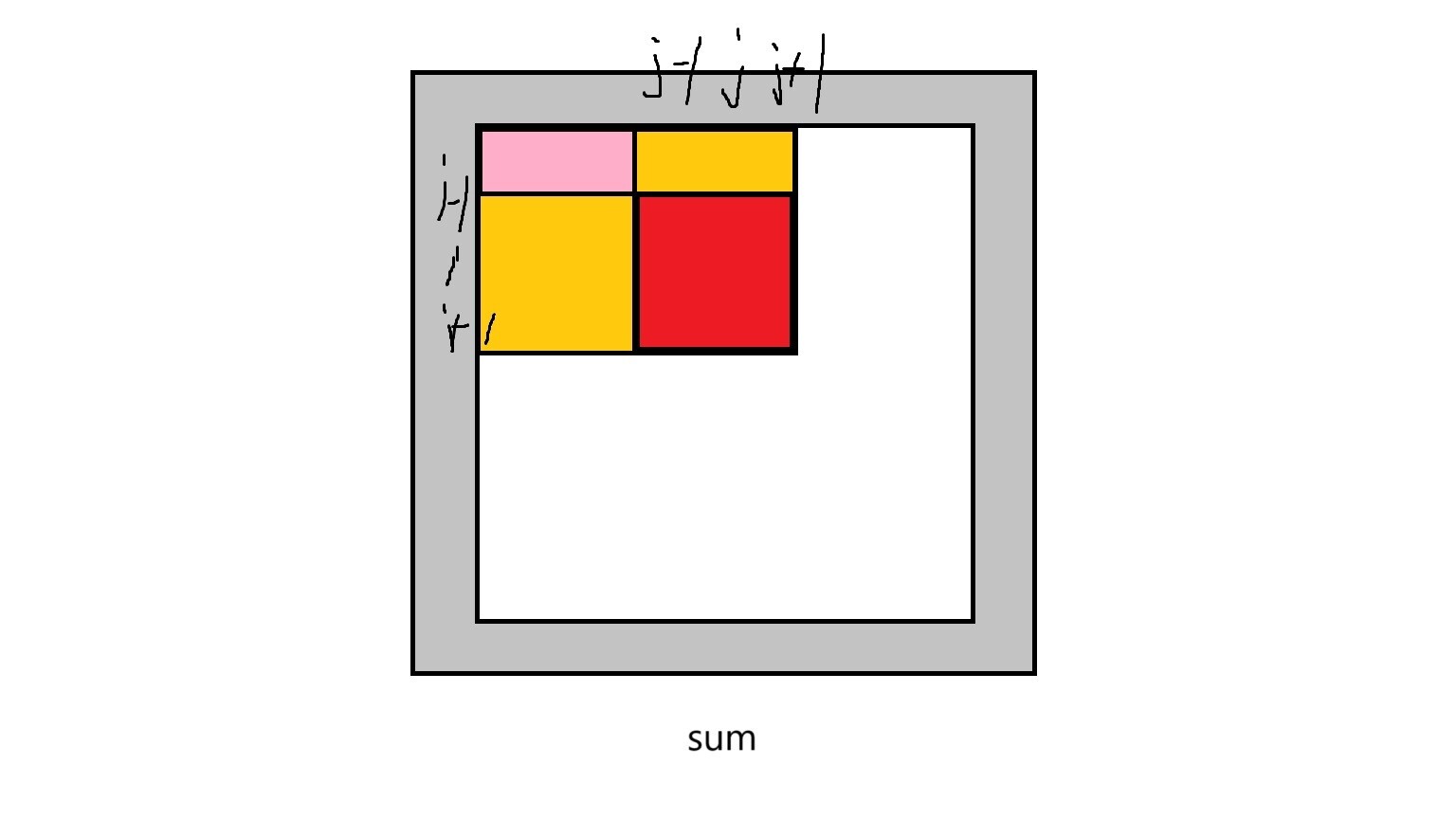
在计算矩阵$img$ 以下边缘某元素或右边沿某元素为中心的平滑器中元素的和时，由于本题$img$ 矩阵和$sum$ 的对应关系与板子中的不同，若用板子里边的$sum[m+1][n+1]$，会导致下标无效（此时下标$i>=m+1$ 或$j>=n+1$），所以这里$sum$ 的大小改为了$sum[m+2][n+2]$。

之后定义四个变量$a,b,c,d$ 分别代表平滑器的上，下，左，右四边界，并以此求出平滑器中有效的元素有多少个，方便求平均值。如果$a,b,c,d$ 标记的超出矩阵$img$ 范围则置为$0$ 或$m-1$ 或$n-1$，可以用取最小值的操作来实现。这么操作优化掉了遍历计数，且便于访问$sum$ 中的值用于求和。则平滑器的和的表达式可写作：

    int Sum=sum[c+1][d+1]-sum[a][d+1]-sum[c+1][b]+sum[a][b];

平滑器中包含元素的个数可写作：

    int cnt=(c-a+1)*(d-b+1);

将 $Sum/cnt$ 的结果加入答案数组即可。 int 类型相除若有余数则向下取整。

# 完整代码：

class Solution {

public:

    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {

        int m=img.size(),n=img[0].size();

        vector<vector<int>> sum(m+2,vector<int>(n+2,0));

        vector<vector<int>> ans(m,vector<int>(n));

        for(int i=1;i<=m;i++){

            for(int j=1;j<=n;j++){

                sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+img[i-1][j-1];

            }

        }

        for(int i=0;i<m;i++){

            for(int j=0;j<n;j++){

                int a=max(0,i-1),b=max(0,j-1),c=min(m-1,i+1),d=min(n-1,j+1);

                int cnt=(c-a+1)*(d-b+1);

                int tmp=sum[c+1][d+1]-sum[a][d+1]-sum[c+1][b]+sum[a][b];

                ans[i][j]=tmp/cnt;

            }

        }

        return ans;

    }

};

时间复杂度为$O(m×n)$ ，与暴力比有一定的优化，但是由于本题数据量，优化不是很显著（有一次还是做到 0ms 了的，LC 评测机有的慢有的快）。