# 矩阵的创建
-
直接输入法:适用于元素较少的情况。
-
函数创建法.
常用的函数: 1. zeros、ones、eye 分别用来生成全为 0 的矩阵,全为 1 的矩阵和单位矩阵。 2. rand、randi、randn 分别用来创建均匀分布的随机数、均匀分布的随机整数和标准正态分布的随机数。%{宇宙安全声明:
这里仅仅举出每个函数常用的例子,更多用法参见 MATLAB 的 help 文档。
%}zeros(100);
% 生成了一个大小为 100*100,元素全为 0 的矩阵。zeros(100,99);
% 生成了一个大小为 100*99,元素全为 0 的矩阵。说明 matlab 支持函数重载。% zeros 默认元素数据类型是 double,如果要指定元素类型,添加对应参数,具体参见 help 文档。ones(100); ones(100,99);
% 生成元素全为 1 的矩阵,其余功能与 zeros 相同。eye(100);eye(100,99);
% 生成一个单位矩阵。其余功能与 zeros 相同。单位矩阵:主对角线元素为 1,其余元素都为 0。a=rand(100);
% 生成一个 100*100 的随机数方阵,每个元素都在 0 到 1 上均匀分布。rand(5,6);
% 生成一个 5*6 的随机数方阵,每个元素都在 0 到 1 上均匀分布。randi([1,5],10,11);
% 生成一个 10*11 的随机数方阵,每个元素 都是整数 且在区间 [1,5] 上均匀分布。randn(5,6);
% 生成一个 5*6 的随机数方阵,每个元素 都是整数 且满足标准正态分布。 -
导入本地文件的数据.
支持的格式:txt.dat\csv\xls\xlsb\xlsm
xlsx\xltm\xltx\ods
# 矩阵元素的修改与删除
# 修改
- 直接用等号赋值的方法对矩阵中引用位置的元素进行修改。
- 使用线性索引(单下标的索引)方式对矩阵的元素进行修改。
注意:如果赋值时将一个或多个元素置于矩阵现有行列元素的边界之外,则会将矩阵的大小进行拓展,MATLAB 会将没有赋值的位置的元素自动用 0 填充,使矩阵保持完整的矩形。
创建一个矩阵 A:
A=[1:4;2:5;3:6]; |
此时 A 的如下表表示:
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
修改第二行第三列的元素:
A(2,3)=10; |
修改后的 A 的如下表表示:
| 1 | 2 | 3 | 4 |
| 2 | 3 | 10 | 5 |
| 3 | 4 | 5 | 6 |
修改第二行的元素:
A(2,:)=10; |
修改后的 A 的如下表表示:
| 1 | 2 | 3 | 4 |
| 10 | 10 | 10 | 10 |
| 3 | 4 | 5 | 6 |
分别修改第一行,第三行的第一列和第二列元素:
A([1,3],[1,2])=0; |
修改后的 A 的如下表表示:
| 0 | 0 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 0 | 0 | 5 | 6 |
空括号中的两个参数,前面的叫做行索引,后面的称为列索引,可以看作一个元素为 * 要被修改的元素的下标 * 组成的集合(也可以看作数组或者向量)。
线性索引:
A(3)=0; |
修改后的 A 的如下表表示:
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 0 | 4 | 5 | 6 |
A(4)=0; |
修改后的 A 的如下表表示:
| 1 | 0 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
在现有矩阵外的某个位置进行赋值:
A(5,6)=666; |
修改后的 A 的如下表表示:
| 1 | 0 | 3 | 4 | 0 |
| 2 | 3 | 4 | 5 | 0 |
| 3 | 4 | 5 | 6 | 0 |
| 0 | 0 | 0 | 0 | 666 |
# 删除
-
套用修改元素的语法,将等号右侧换成空向量
[],即可删除对应的元素。注意,这种方法通常只能删除整行或整列的元素,否则会报错。 -
或者使用线性索引来删除矩阵的元素。使用线性索引删除后,MATLAB 会将矩阵中剩下的元素按线性索引的顺序放入一个向量中。使用线性索引可以删除任意位置的元素,不需要删除矩阵的一整行或一整列。
仍然拿修改部分的 A 矩阵举例:
A(:,1)=[]; |
运行代码后的 A 矩阵如下表表示:
| 2 | 3 | 4 |
| 3 | 4 | 5 |
| 4 | 5 | 6 |
使用线性索引:
A(1)=[]; |
运行代码后的 A 矩阵如下表表示:
| 2 | 3 | 4 | 2 | 3 | 4 | 5 | 3 | 4 | 5 | 6 |
可以看到执行代码后删除了第一个元素的同时也将原矩阵转换成了一个向量。要想删除后保持原矩阵的样子,要使用 reshape 函数,后面讲。
# 矩阵的拼接与重排
# 矩阵的拼接
-
横向拼接:
要求 A 和 B 行数相同。使用:[A,B];
[A B];
cat(2,A,B);
都能将 A,B 横向拼接成一个大矩阵。
-
纵向拼接:
要求 A 和 B 列数相同。使用:[A;B];
cat(1,A,B);
都能将 A,B 纵向拼接成一个大矩阵。
A=[1:5]; | |
B=[6:10]; | |
C=[A,B] | |
D=[A B] | |
E=cat(2,A,B) |
运行结果:
C = 1 2 3 4 5 6 7 8 9 10
D = 1 2 3 4 5 6 7 8 9 10
E = 1 2 3 4 5 6 7 8 9 10
A=[1:5]; | |
B=[6:10]; | |
C=[A;B] | |
D=cat(1,A,B) |
运行结果为:
C =
1 2 3 4 5
6 7 8 9 10
D =
1 2 3 4 5
6 7 8 9 10# 矩阵的重排
- reshape 函数:更改矩阵的形状,用法:
reshape(A,m,n) |
或
reshape(A,[m,n]); |
A=randi([0,6],2,6); | |
B=reshape(A,3,4); | |
C=reshape(A,3,4); |
运行结果如下所示:
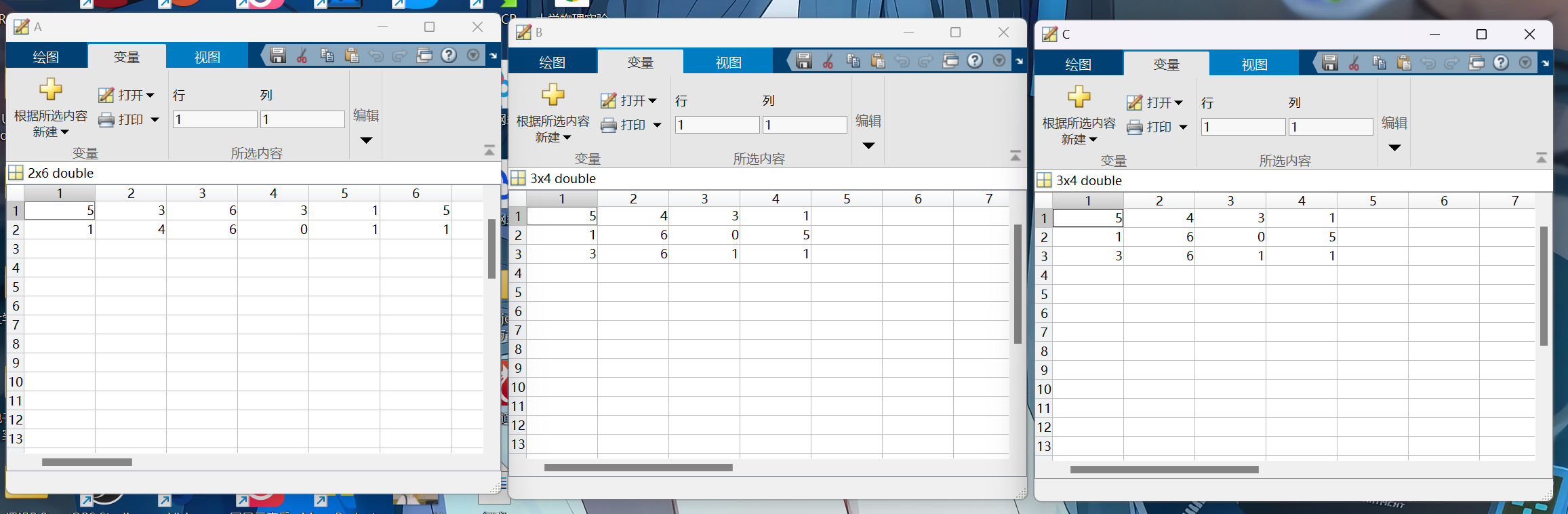
可以发现重排时按照线性索引对函数进行重排,即一列一列地放。
- sort 函数:对矩阵或者向量进行排序,sort (A,dim), 最后面加一个参数
decscend,变成降序排列。- dim=1 沿着行方向(上到下)对矩阵每一列进行升序排列。
- dim=2 沿着列方向(左到右)对矩阵每一行进行升序排列。
A= randi([1,50],3,4); | |
B=sort(A,1); | |
C=sort(A,2); |
运行结果如下所示:
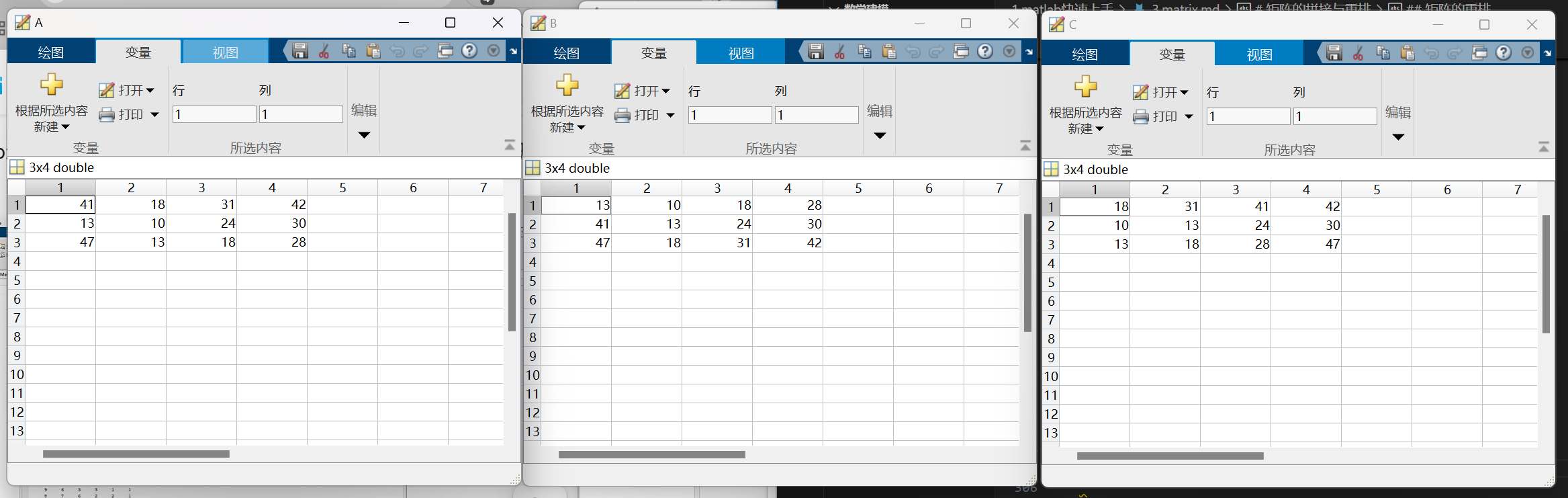
- sortorws:基于某一列对矩阵进行排序,同一行元素不变。用法:sortrows (A, 某列的索引),在最后面加
descend,变成从大到小的降序排列。
$e.g. $
A= randi([1,50],3,4); | |
B=sortrows(A,2); |
运行结果如下所示
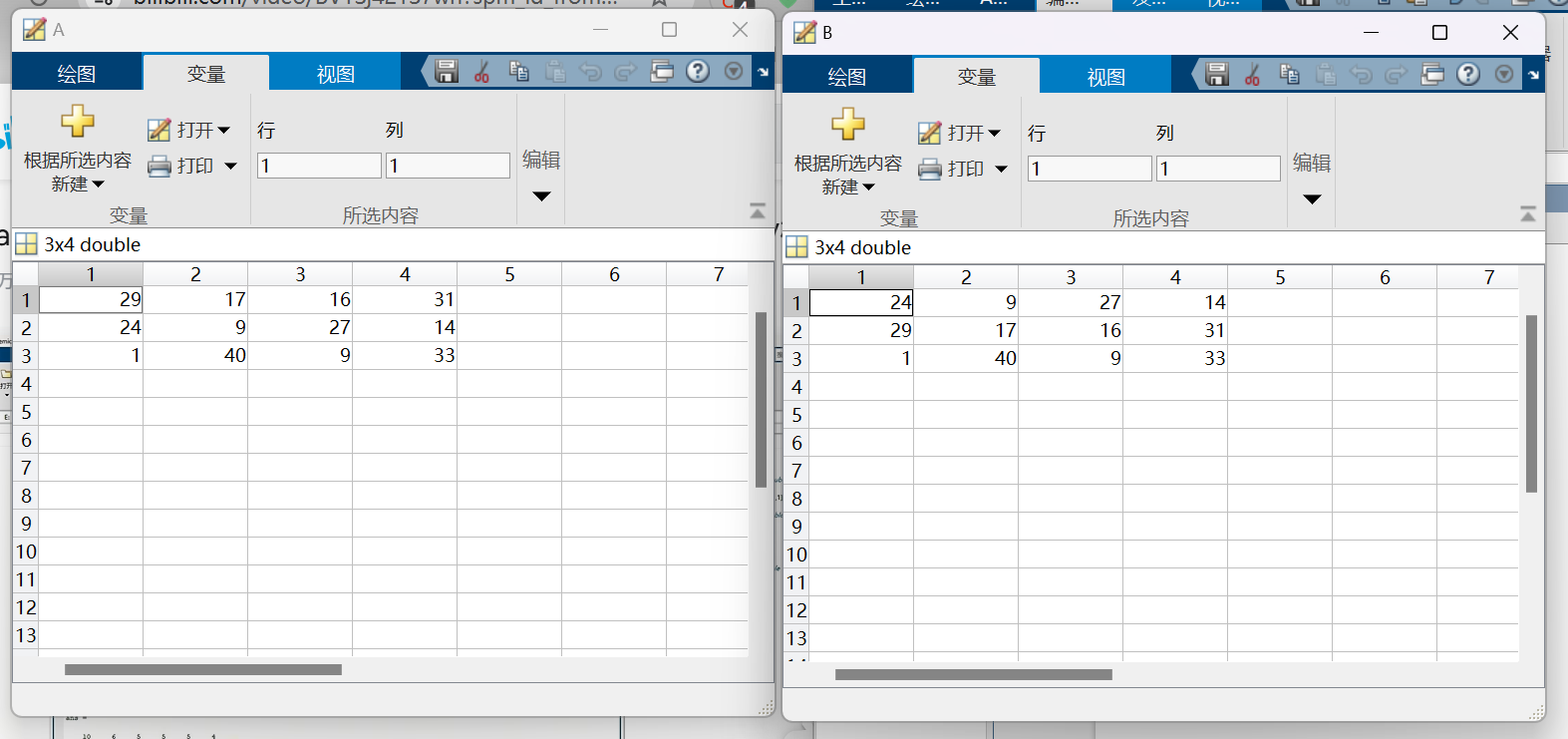
# 矩阵的运算
# 调用函数运算
| 函数名 | 功能 |
|---|---|
| sum | 矩阵求和函数 |
| prof | 矩阵求积函数 |
| cumsum | 计算 A 的累计和 |
| diff | 计算差分 |
| mean | 计算平均值 |
| median | 计算中位数 |
| mode | 计算众数 |
| var | 计算方差 |
| std | 计算标准差 |
| min | 求最小值 |
| max | 求最大值 |
具体用法请查阅 help 文档
# 矩阵的算术运算
# 矩阵加减
与线性代数知识稍有不同,MATLAB 中矩阵加减运算不需要参与运算的两矩阵大小完全相同。而是符合 MATLAB 矩阵算术运算的五种兼容模式即可。如下图所示:
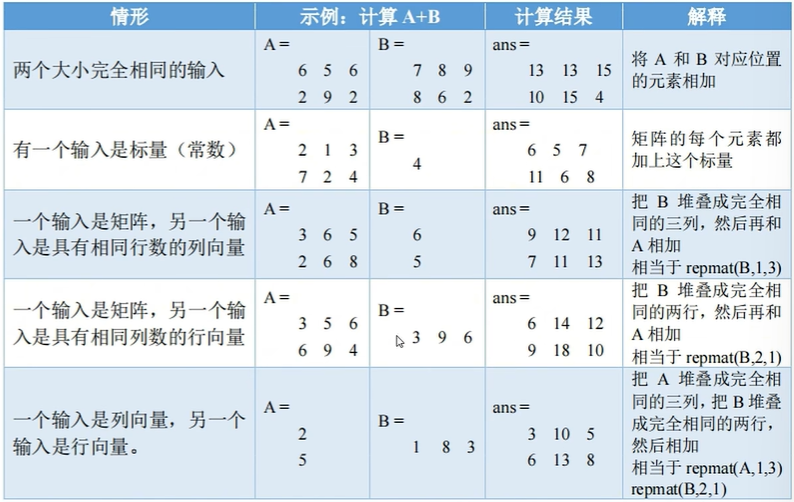
# 矩阵乘除乘方
* 表示矩阵的乘法,运算规则等和线性代数的知识符合。
.* 表示矩阵对应位置元素相乘。矩阵大小满足上面的五种兼容模式。
$e.g. $
A= randi([1,50],3,4); | |
B= randi([1,5],4,4); | |
C=A*B; |
运算结果如下图所示:
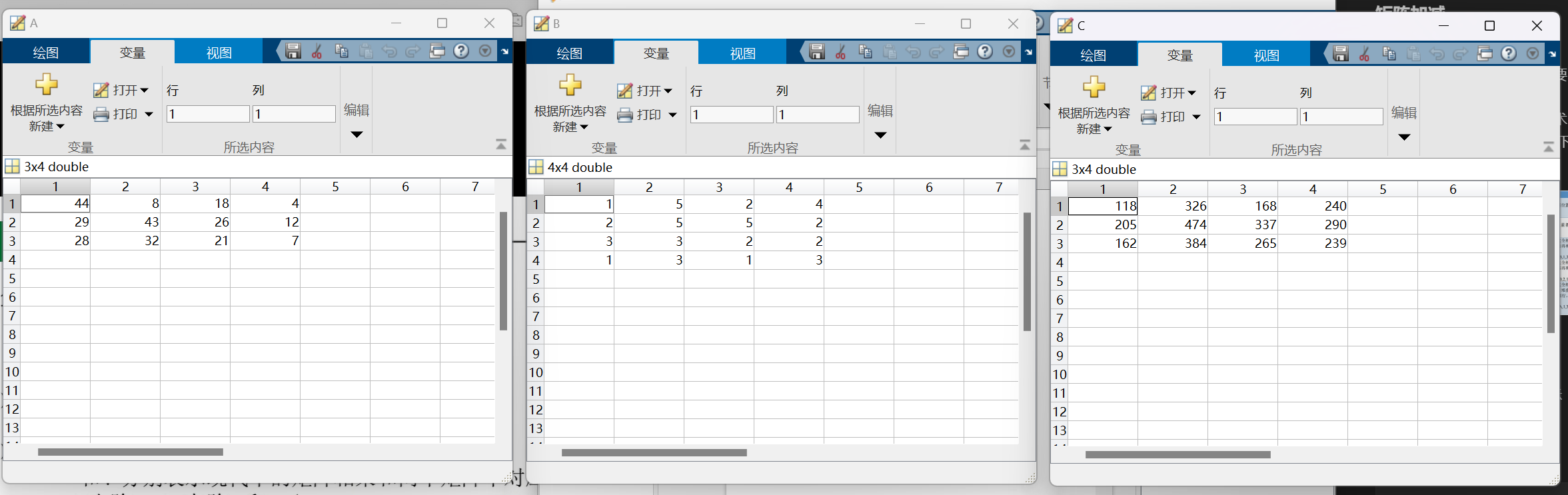
===
众所周知线性代数没有除法只有逆矩阵相乘。而 MATLAB 中定义了矩阵的除法。
/ (右除)
\ (左除)
以上两种运算用于求解方程组,使用率较低,使用的时候可以参见 help 文档。
.\ (点除)对应元素相除。运算时要满足五种兼容模式。
^ 定义了矩阵的幂运算。
.^ 对应位置求幂。
# 矩阵的转置
' 定义了矩阵的转置。转置即矩阵行列互换。
当矩阵元素中含有复数时,对矩阵求转置会把其中的复数元素求共轭。
而 .' 则会在求转置之后将原复数保留在矩阵中。
# 矩阵的逻辑运算
== |
~= |
> |
>= |
< |
<= |
|---|---|---|---|---|---|
| 等于 | 不等于 | 大于 | 大于等于 | 小于 | 小于等于 |
关系运算符可以表示两个数组中元素的关系,如果比较的结果为真,返回 1,否则返回 0。